Ethereum Foundation's $1 Million Bounty for Proving the Up-to-Capacity Proximity Gaps Conjecture

During a recent episode of the Zero Knowledge Podcast, Justin Drake, a researcher at the Ethereum Foundation, announced a $1 million bounty for proving or disproving the "up-to-capacity proximity gaps conjecture for Reed-Solomon codes", specifically its strengthened "mutual correlated agreement" variant. This conjecture is fundamental to the security and efficiency of hash-based SNARKs used in ZKP’s, which are central to Ethereum's scaling roadmap. If proven, it would solidify the foundations of modern ZK systems; if disproven, it could necessitate redesigns, increasing proof sizes and computational costs.

This article examines the conjecture's nature, its significance, and its impacts on the Ethereum ecosystem and beyond.

What It Is: Defining the Conjecture

The up-to-capacity proximity gaps conjecture pertains to Reed-Solomon (RS) codes, a class of error-correcting codes widely used in cryptography, particularly in interactive oracle proofs (IOPs) of proximity like FRI (Fast Reed-Solomon IOP of Proximity).

RS codes are algebraic constructs over finite fields that encode messages into polynomials, enabling detection and correction of errors in data transmission or storage.

Core Concept: Proximity Gaps in RS Codes

A "proximity gap" in coding theory refers to a binary outcome for a tester querying a purported codeword: either the word is close to a valid RS codeword (within a small relative distance δ), or it is far from all valid codewords (beyond a larger distance). Existing results, such as those in the 2020 paper "Proximity Gaps for Reed–Solomon Codes" by Eli Ben-Sasson, Kopparty, and Saraf, demonstrate that for RS codes of rate ρ (ratio of message length to codeword length), proximity gaps exist up to half the minimum distance (roughly δ = (1 - ρ)/2). This means testers can distinguish close vs. far codewords with high probability using few queries.

The conjecture extends this gap "up to capacity," meaning it holds for proximity parameters approaching the full Singleton bound (δ approaching 1 - ρ).

In practical terms, if a word is within δ of an RS codeword, the tester accepts; otherwise, it rejects with high soundness. The "capacity" refers to the maximum error rate where unique decoding is possible.

Strengthened Variant: Mutual Correlated Agreement

The bounty targets the "mutual correlated agreement" version of the conjecture, as used in advanced FRI variants like WHIR (a Reed-Solomon proximity testing protocol with super-fast verification). This strengthening assumes that if a random linear combination of functions is close to a codeword in a code C, then the individual functions must each be close to correlated codewords. It builds on the standard "correlated agreement" used in earlier FRI protocols, adding a "mutual" property to support recursion and smaller proofs in hash-based SNARKs. Experts believe mutual correlated agreement holds if standard correlated agreement does, but formal proof is lacking.

In Ethereum's context, this conjecture is assumed in zkVMs for real-time proving of Ethereum blocks, enabling L1 scaling without re-execution.

Why It Matters: Significance in Cryptography and Blockchain

The conjecture is essential to efficient ZKPs. In blockchain, these proofs enable scalability by compressing computations into verifiable proofs.‍

Cryptographic Importance

Efficiency in SNARKs: Hash-based SNARKs like those in FRI rely on the conjecture to achieve small proof sizes (reduced by ~2x) and low query complexity. Proving it would validate these optimizations; disproving it could introduce vulnerabilities, forcing larger proofs and higher latency.
Post-Quantum Security: WHIR and similar protocols are hash-based, making them resistant to quantum attacks, unlike lattice-based alternatives. The conjecture supports recursion for aggregating signatures, crucial for Ethereum's post-quantum upgrades.
Broader Math Implications: Comparable to Millennium Problems, resolving it advances algebraic coding theory and could influence fields like quantum computing and AI verifiability.

Blockchain and Ethereum Relevance

Ethereum's "snarkify everything" roadmap depends on real-time ZK proving for L1 scaling to 1 gigagas/second (10,000 TPS) and L2s to 1 teragas/second (10M TPS). The EF firmly recognizes ZK's role in achieving this, but without proven conjectures, ZK adoption risks stalling.

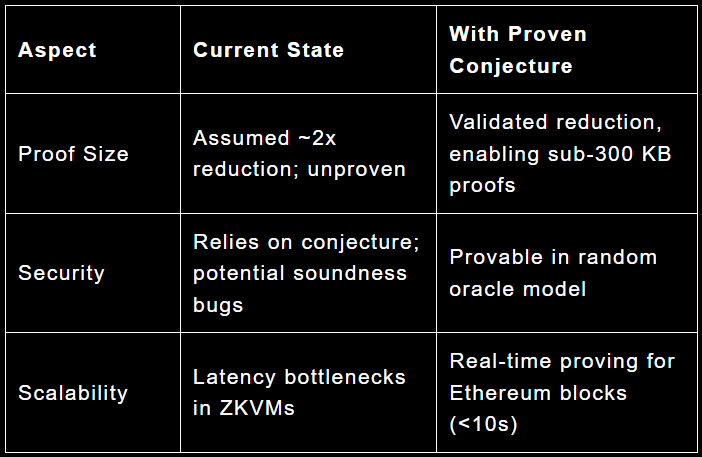
What It Affects: Impacts on Ecosystems and Technologies

Direct Impacts

zkVMs and Provers: Nearly all 32 zkVMs tracked by Ethproofs (e.g. SP1, Ziren, etc) assume the conjecture for hash-based proving. Disproof would require doubling proof sizes, increasing costs from ~1 cent/block to higher, affecting networks like Succinct's Prover Network.
Ethereum Upgrades: Affects Pectra (2026) and beyond, including mandatory proofs and RISC-V enshrinement. Could delay L1 scaling and blob throughput increases.
Privacy and Composability: Impacts wormholes for private transactions and cross-rollup safety.

Broader Effects

Competing Ecosystems: Many projects could face redesigns.
Non-Blockchain Applications: Influences AI agents (verifiable computations) and high-integrity systems (e.g. banking, aeronautics), potentially creating multi-billion-dollar markets for ZK hardware like Nvidia's ZPUs.
Economic Ramifications: Proving markets could reach billions of dollars annually if ZK replaces economic security in chains like Sui ($660M/year).

Bottom Line for Readers‍

This bounty makes a quiet assumption into a binary test. When you evaluate ZK stacks, ask:

1. Do they rely on mutual correlated agreement up to capacity and at which code rates/query budgets?
2. What are proof-size and latency if that gap tightens by ~2×?
3. What fallback (alternative IOP/PCP or code family) is implemented if a counterexample appears?

A resolution - either a proof with explicit constants at deployed parameters or a high-rate RS counterexample - will reset performance claims across Ethereum and adjacent systems. Until then, treat “real-time, post-quantum, recursive” results as conditional on this conjecture.

‍